计算机系统工程之:AI计算与训练优化
Weiquan HuangDistributed (and parallel) programming
前面讲了很多,都是关于AI需要庞大计算量的引子,引出后续针对如何加快计算速度的策略讲解
比如训练一个神经网络,前向和后向的一次迭代总共是6倍的$sizeof(W)*B$,$W$为矩阵元素个数,$B$为自变量特征数,注意这里的$W$是所有层的参数
parallelism in single node
- 首先多核(多线程)的计算效率肯定高于单核单线程,单核的问题在于流水线的制约,可以改良流水线以及加快CPU处理一个指令的速度
- 多核的问题是:每个核有自己的L1/2缓存,而缓存的数据来源于内存,但是每个核的缓存有可能是不与内存完全同步的,就导致了计算结果正确性不能保证(设计cache coherence protocols,比如单个核缓存更改后广播至其他核,或者只广播(或者全局版本号dir)已修改数据的版本号等要拿的时候再去对应的核拿最新数据);这个缓存一致性问题严重制约了当前处理器增加核数所带来的性能提升/通过增加开发者开发难度的方式实现有限的保证缓存一致性的方法
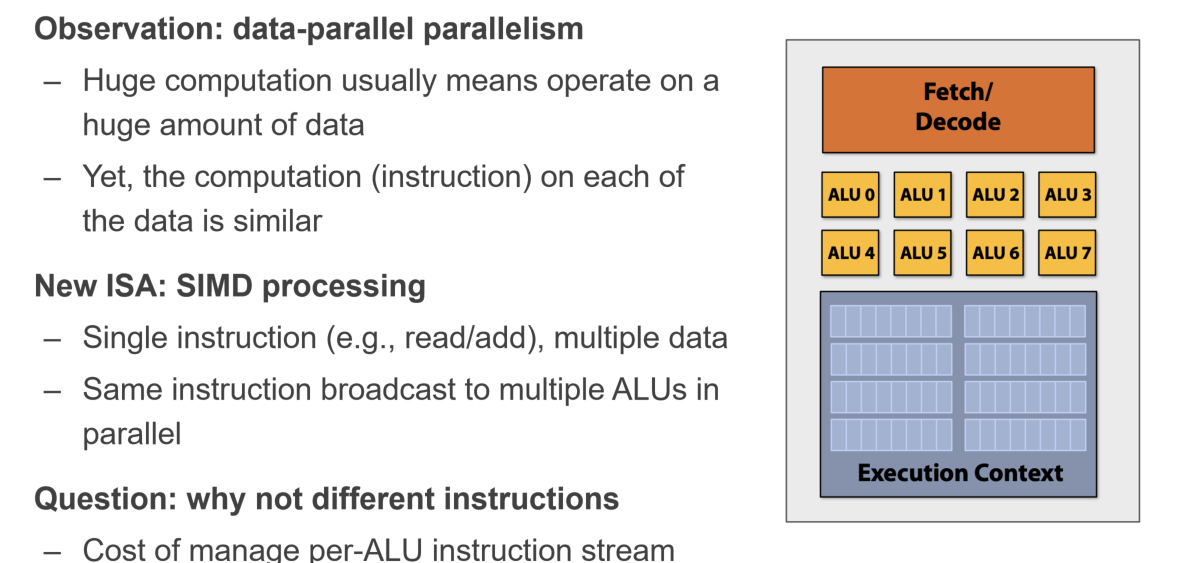
- 增加每个核的计算单元ALU,也可以同时处理互相之间无关的计算指令(不能同时处理有互相依赖的指令),比如SIMD就有给C++添加适配于单核多计算单元的接口,能够让一个指令执行多个浮点数的计算;但是其实无法达到理想的增加几倍的ALU就增加几倍的效率,这取决于计算指令之间的互相依赖关系、访存时间与纯寄存器计算的时间差异(木桶效应),所以这里的制约是CPU访问内存的“位宽”(主要影响原因是从CPU到内存的延迟)
accessing memory
访存时间取决于两个因素:访问延迟+位宽
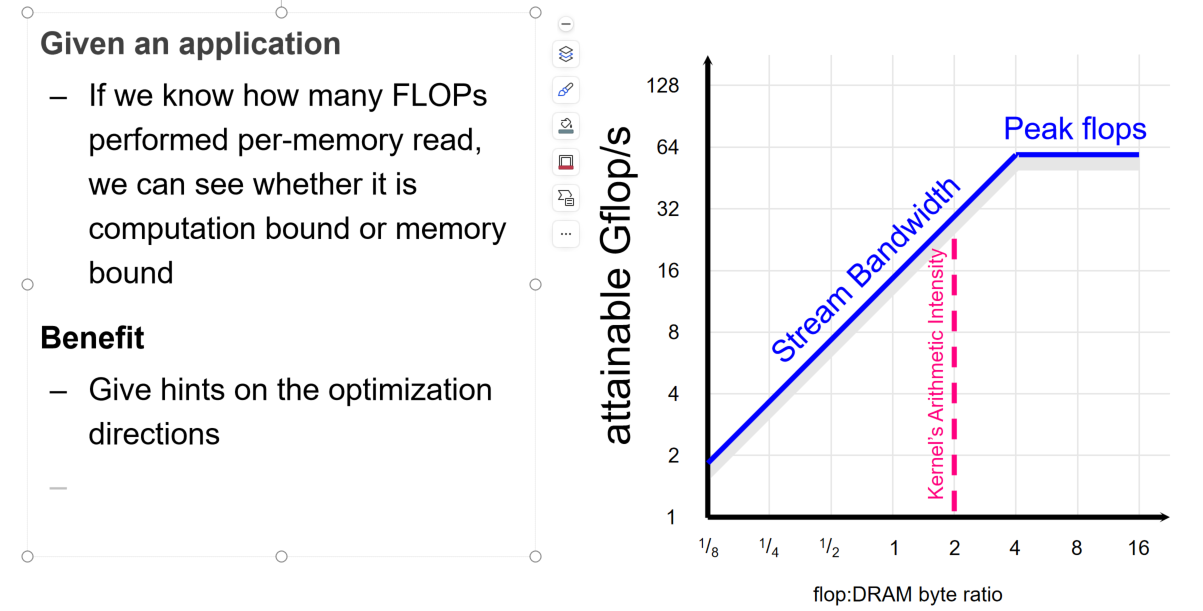
每个设备有自己的Peak Flops,表示设备最快能够每秒执行多少个浮点计算;OI(Operation Intense)表示对于某个浮点计算任务,每访问一个Byte能够执行多少个浮点运算(比如假设1个浮点数为2Byte,那么两个不同的浮点数计算需要4Byte,那么OI=1/4);在OI比较低的时候,性能受限于系统的带宽,因为可以认为CPU/GPU处理计算任务和访问内存是同时进行的,在OI较低的时候就意味着访问内存的时间高于CPU/GPU处理计算任务的时间,CPU/GPU在一定时间内为空闲等待状态,那么就相当于系统性能受限于带宽,而带宽为Peak Flops/OI(可以从单位推导);反之,OI较高的时候就取决于CPU/GPU的计算速度,那么就是受限于硬件的极限了
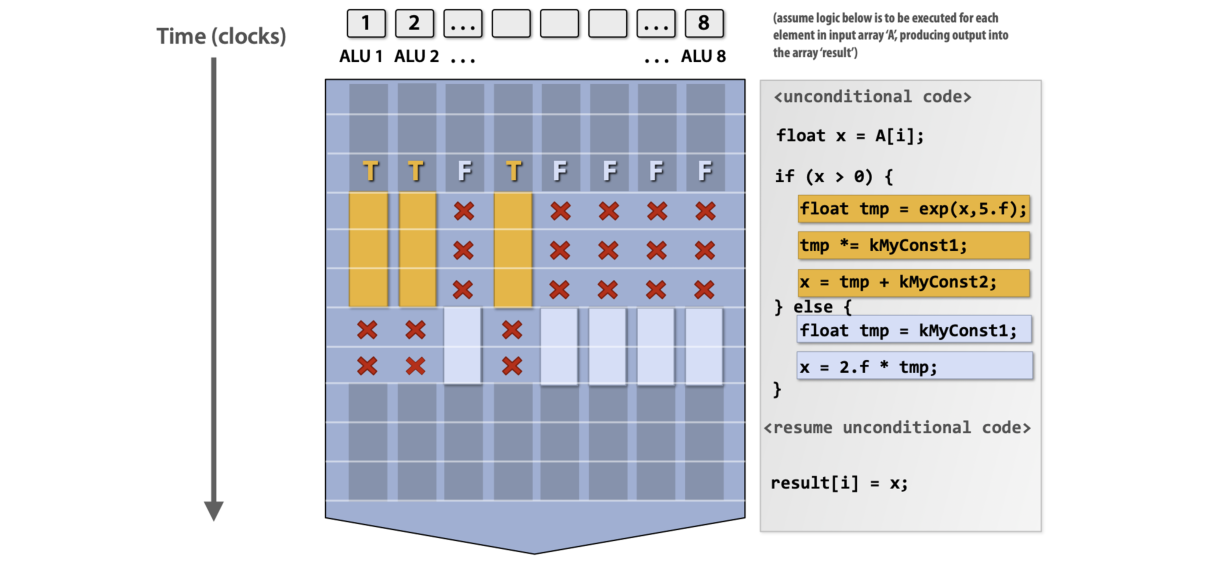
单纯靠SIMD的机制仍然无法满足需求,比如如果出现了带分支的计算,那么常规情况下由于无法判断每个元素要怎么计算,因此会从并行退化成串行;不过SIMD有自己的解决方式,就是将两个分支的结果都算一遍,然后通过条件判断式保留正确计算过程的结果(mask),虽然会有被浪费掉的计算资源,但是至少并行是被充分利用的
改良方法SIMT:单个指令由多个线程执行,每个线程执行相同的代码,但是这段代码对不同的数据进行了分支判断和计算正确分支,统一block直到所有线程执行完毕
MapReduce
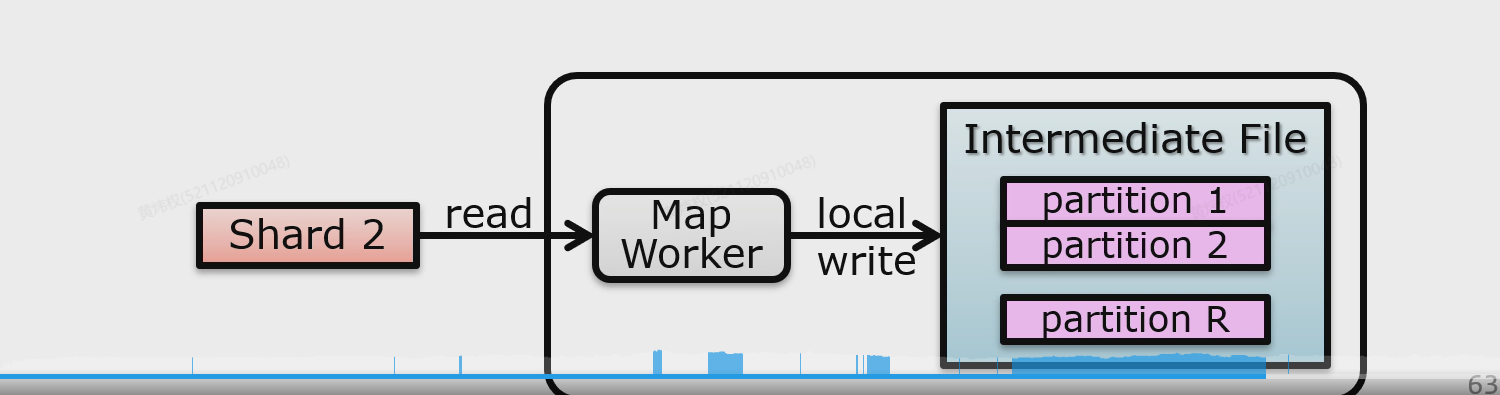
感觉就是Map是将数据分成几个块,每个块单独处理,成为映射;Reduce就是汇总Map的信息,然后计算出总的结果;比如数单词个数,就可以先数每个单词在各自文件的个数,然后再统一汇总起来;不过在Map发给Reduce的中间文件最好对其进行sort,这样Reducer可以获取到比较集中的数据(相同key的数据尽可能在同一个位置),方便于后续Reducer的数据集中;同时Reducer最好也对来自不同Map的文件进行merge sort,算是一个小优化
Map之前也需要把要处理的文件进行shard分片,而由于文件是在GFS体系中存储,因此最好设置shard size为GFS的chunk size,这样可以尽最大的努力让尽可能少的RPC请求传输最多的数据;Map也会将中间结果分片,不同的片针对不同的Reducer,这样就可以让不同的Reducer尽可能少地进行random access,提取出需要让这个Reducer做的数据,而不是让这个Reducer去扫
Fault Tolarance:把文件存在类GFS的系统里,对于暂时失效的worker重启并且重新执行即可,同一个任务做两遍其实只需要覆盖就行了,他也不需要担心误判失效带来的重复计算的问题;如果master挂了,最好是master把自己的执行日志通过checkpoint机制来存放到GFS系统中,这样重启或者新开一个master之后就不会出现要重新执行之前已经执行的任务的情况了;如果worker执行的时候出现了错误,比如因为文件格式问题出现SegFault,那么一般是master直接让这个worker丢弃这个任务,做下一个
Locality:每个节点都从GFS读取文件数据,那么会比单纯靠网络传输要快,MapReduce在GFS文件系统上运行
Redundant Execution:如果一个worker很慢会让别的worker陷入等待,可以采用多个worker执行同一个任务来进行备份,从而只要有一个备份完成了就可以继续,但是这对资源比较稀缺的AI计算还是不太现实的方法,也有可能就先暂时放任他这么慢了
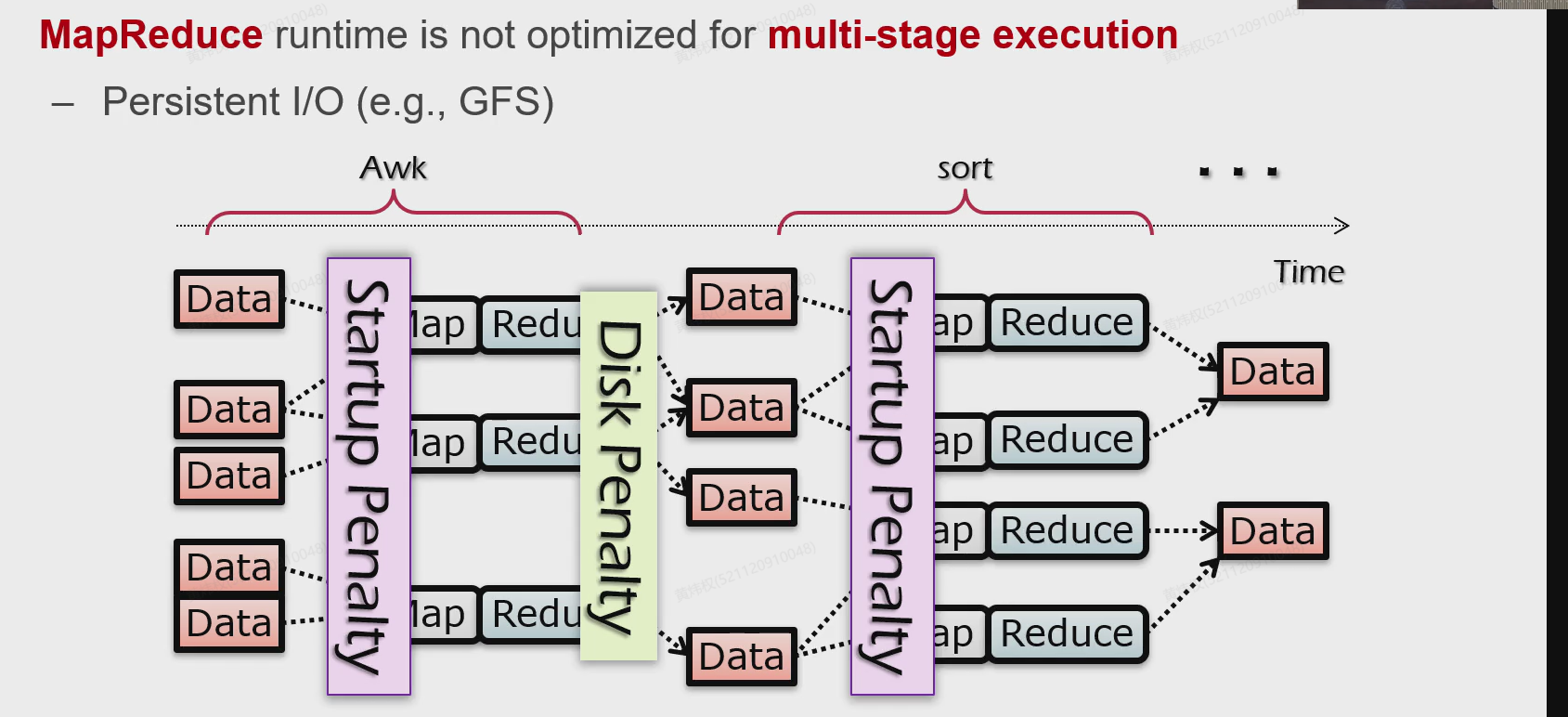
不建议只有一个MapReduce集群的系统对多个任务进行类流水线的MapReduce流,因为这会造成下面两种Penalty,比如非最后阶段的Reduce产出的结果其实没必要写到磁盘里,但是只有一个MR体系就意味着没有能够接盘的其他体系;而且一个MR针对不同的任务也要做初始化,这其实和串行也没什么差了,没有发挥出流水线的作用
MapReduce可以抽象成“多分图”(二分图的扩展版本hh),很多都可以从MapReduce推出
Computation Graph
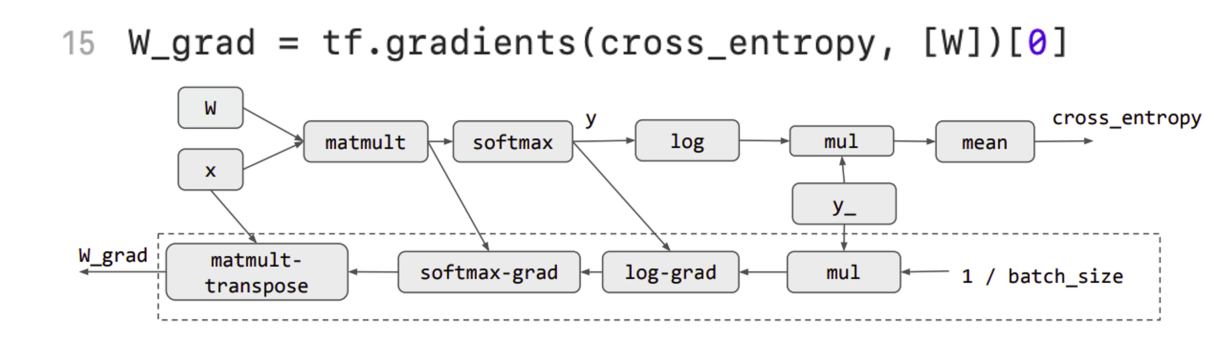
在机器学习模型的训练过程中,可以将这些训练过程中常用的操作记录为计算图的一个节点,使用计算图的好处有:记录中间结果,以方便反向传播计算梯度用于拟合、不同的硬件会为相同的深度学习计算图节点实现不同的底层汇编逻辑
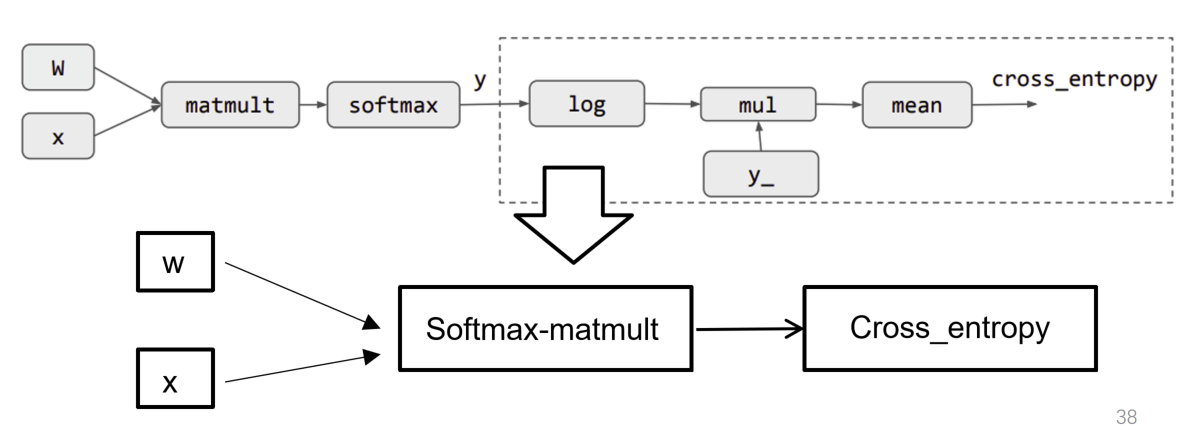
一般来说,CPU将要计算的内容和计算图的节点发送给GPU让其去计算,GPU将结果发回给CPU;这里面就涉及到了访存的开销,CPU将数据和算子发送也是需要开销的;于是就产生了两个合并算子的流派:第一种是将几个经常连在一起的算子合并成一个大算子发送给GPU,这样做的缺点是比较难以编程;第二种是将多个算子打包发送,在GPU上再拆解并逐步计算(英伟达)
Distributed Training
Data Parallelism
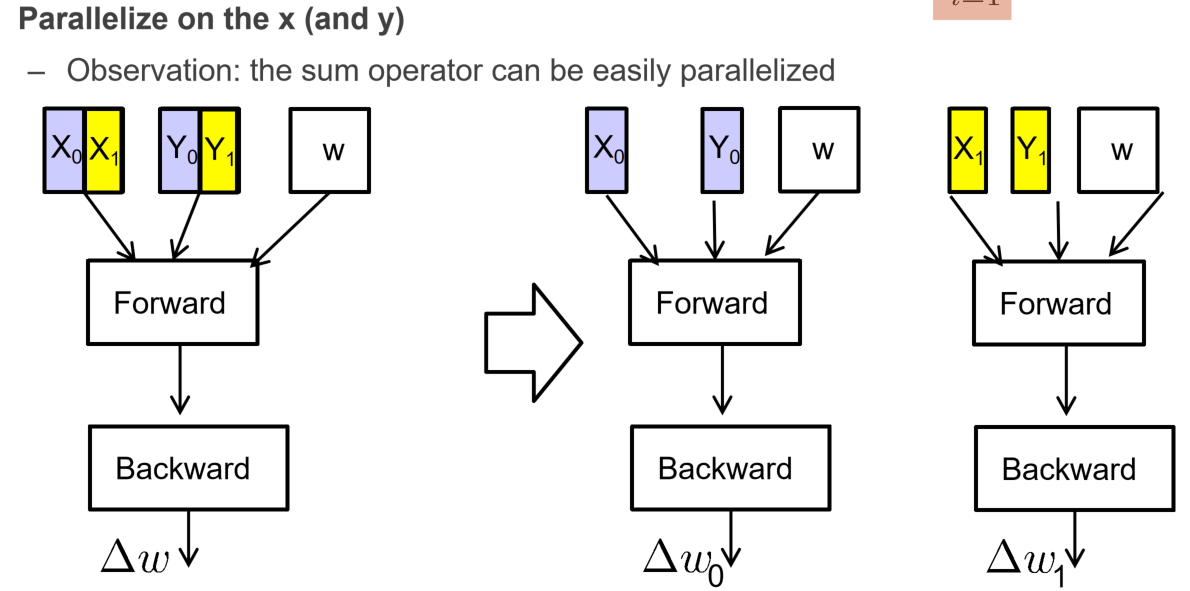
在计算梯度的时候,首先要计算损失函数,而这里有一个累加的过程,是可以通过将累加的过程并行化来实现MR的思路的
不过主要的问题其实就是在于,如何将每个节点的$\delta w$给传播出去,从而得到汇总值已进行下一步的计算;同时也会受到木桶效应的影响,即速度最慢的节点会明显让其他节点陷入空闲;用于优化这一流程的技术被称为AllReduce,优化的目标有:减少数据传输的量、以及降低数据在同一时刻大量地打到某个网卡的现象(因为这会极大地拖慢这个网卡对网络数据的吞吐速率)
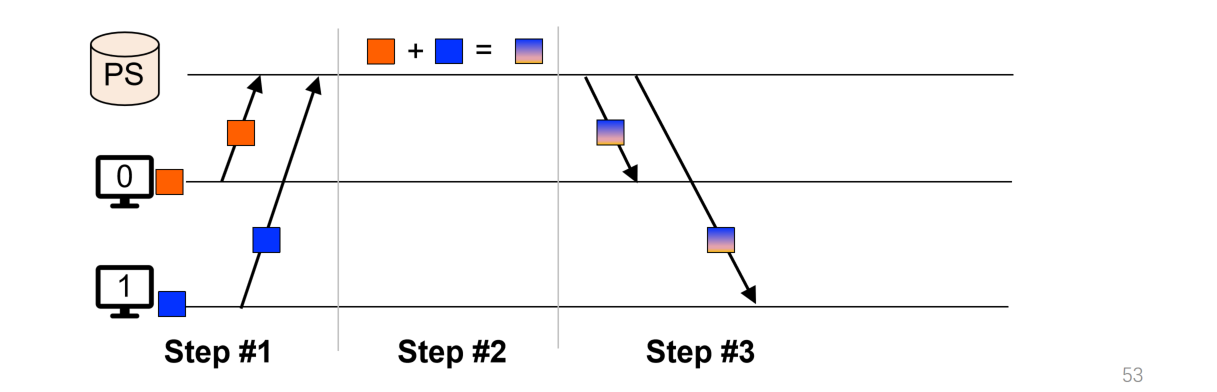
- Parameter Server:用一个中央服务器来接受每个部分的参数来计算总体的值,但是这里的问题是,每个节点都会发送参数大小为$N$的数据(这里的$N$表示的是每个节点携带的参数量),而且有$P$个节点,那么不仅数据传输量比较大,而且对于某一时刻对于PS的负载也会很大;这在上课讲的一个实例中可以看到这种方法即使是计算一个比较小的模型,而且使用最好的网卡,网络传输也是一个很大的瓶颈
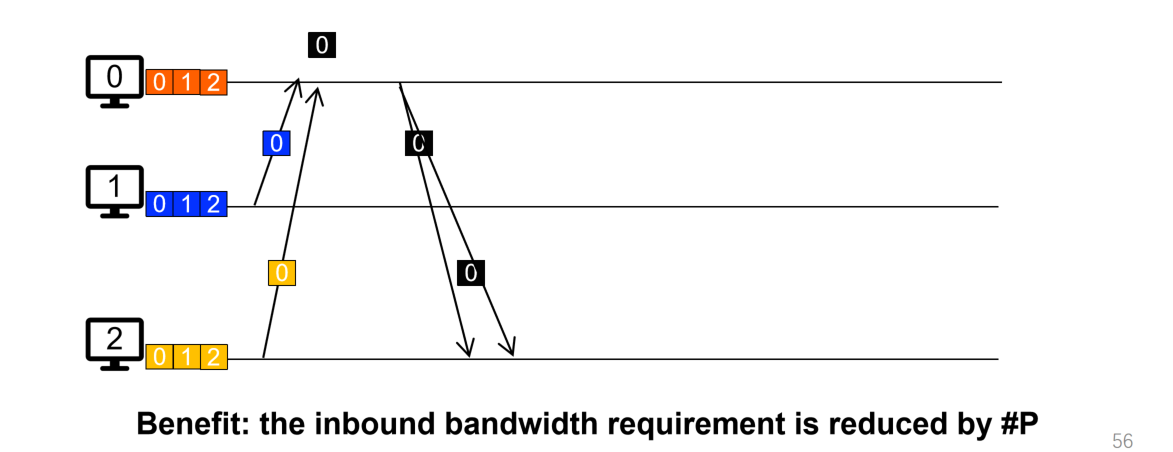
- Sharded PS:将数据拆成$P$个部分,每台机器负责不同的部分,在传输的时候也需要传输对应的部分即可,这样对于接收者来说,其接收到的数据量降低到了$O(N)$的量级,因为只需要接收到自己负责计算的部分,以及其他节点计算好了的他们负责的那部分(原来是$O(PN)$),而且只需要一轮communication,即每台机器训练完成之后就将不同的数据立即分发到不同的机器上,不过这里对于“同一时间涌入网卡的数据量“还是在$O(P)$量级,英文称为fan-in
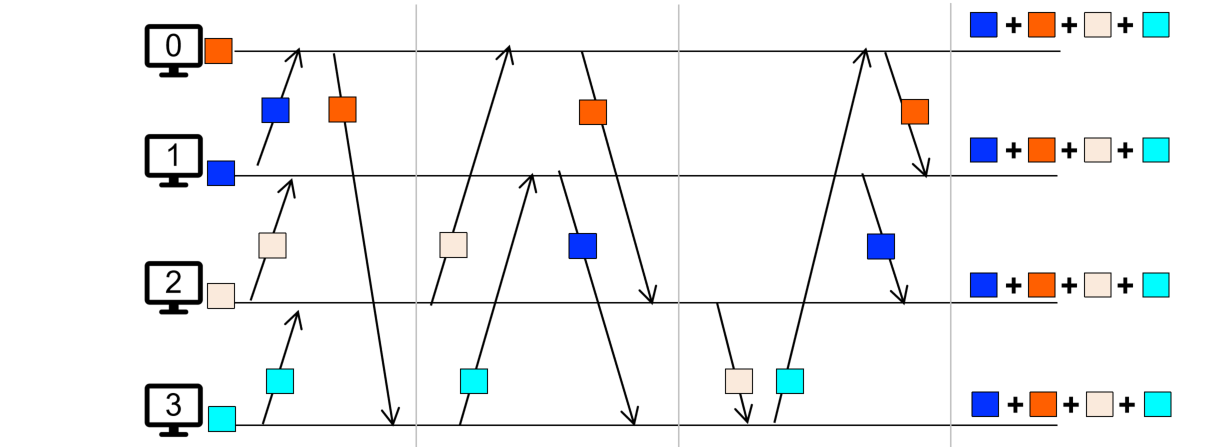
- De-centralized:去中心化,可以采用比较流水线的策略,比如每个节点要发布各自的部分的时候,0->1,1->2,2->3,3->4…,如此交错,对彼此的网卡不影响,单一时间涌入网卡的数据量就是$O(N/P)$,总体的数据接收量是$O(NP)$,不太好,因为这里的思路仍然是汇总之后分别计算
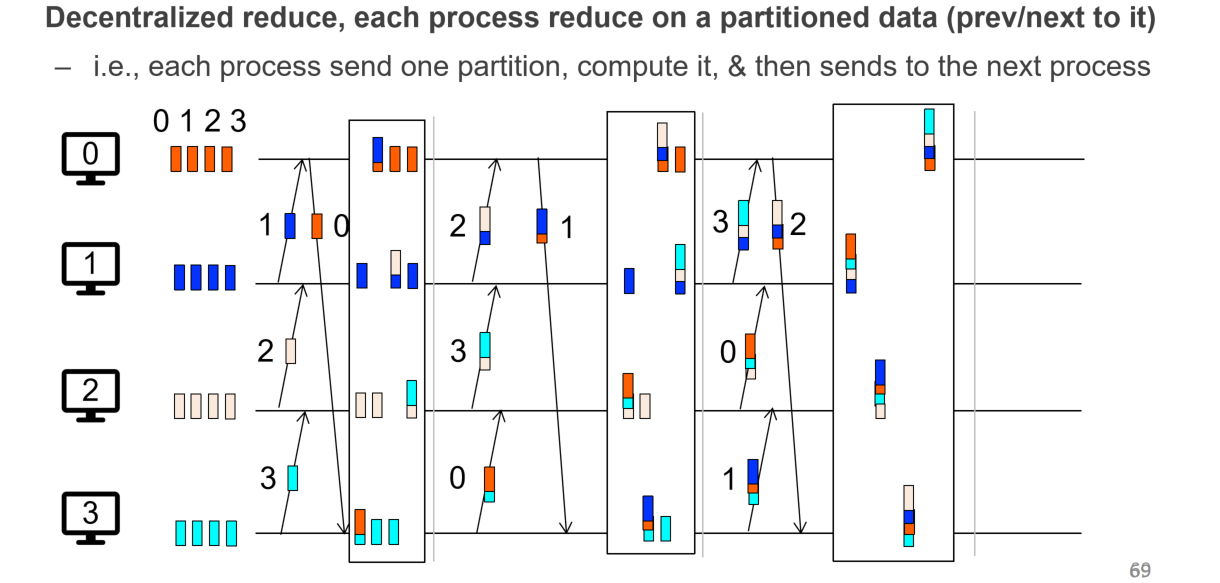
- Ring AllReduce:综合shard和de-centralized,将每个节点的参数继续分成$P$份,用类流水线方法进行传递,传递之后将每个节点汇总好的结果在继续按照流水线的方式进行传递;这样不仅兼顾了shard和de-centralized的好处,而且为了降低每个节点要维护的连接数量,每个节点只需要和相邻的节点进行通信,那么也就只需要维护和相邻之间节点的连接
Ring AllReduce的缺点主要是轮数太多,如果每轮的数据量不多的话其实没什么优势,而且其实在Python的浮点数计算中其实加法是不能结合律的,不同的顺序会有不同的结果,会造成细微的差别!但是这并不影响Ring AllReduce是一个非常好的分布式MR架构
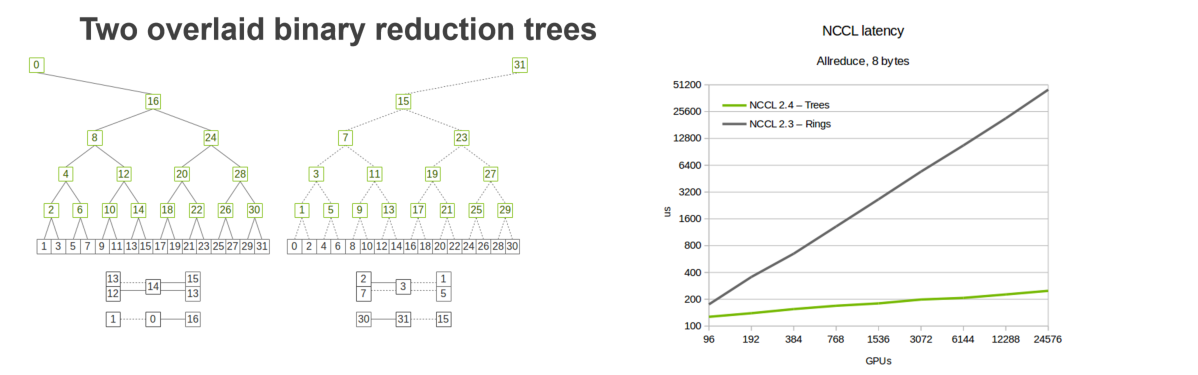
- Tree AllReduce:使用二分法来进行分片,比Ring的P轮加法会更高效一点,相当于将加法做了merge,其效率变成了对数级别的
- 总结
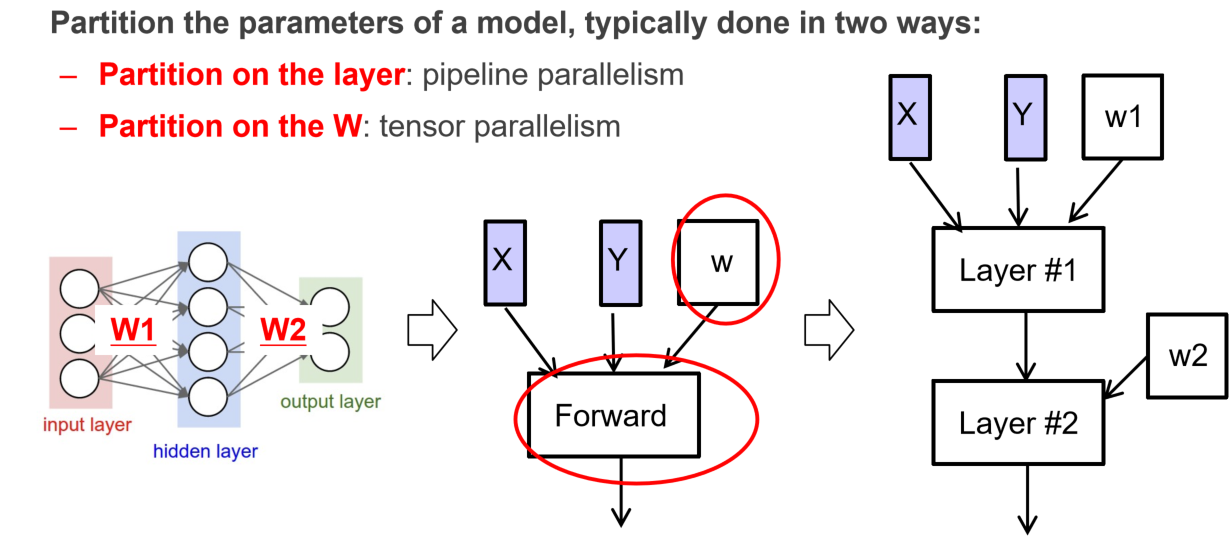
Model Parallelism
模型的训练是可以分层的,每一层可以按照类流水线的方式去分给不同的机器做
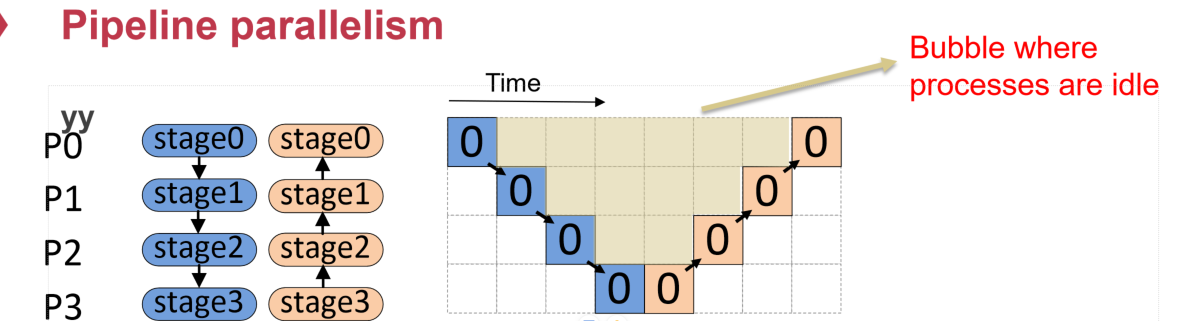
由于前向和后向是具有依赖关系的,最简单的分层就会如图所示出现很多个bubble,造成计算资源的等待和浪费
可以使用这种方法来略微减少一点bubble,毕竟这也算是用到了流水线的思想,只是前向和后向依然无法摆脱依赖
理想情况下,上图应该是一个长方形,所耗时间是batch的轮数和前向、后向传播的耗时,即下图所展示的$m·(t_f+t_b)$,但是由于bubble的出现,导致有$(p-1)·(t_f+t_b)$的时间是空耗掉的(上图中底部没有被有色正方形覆盖的长度),比率为$\frac{p-1}{m}$
更改batch数量是不现实的,因为太小的batch(即m很大),会让之前所讲的GPU的计算资源利用率很低,因为每轮计算GPU可以同时计算较多的数据,batch太小会让这些计算资源没有办法得到充分利用;太大的batch则会导致梯度训练的效率下降,因为batch太大会让模型训练的梯度变小,以一个更慢的速度趋近于极小值
更改p也不是很合理,因为p本身就是因为参数的数量级太大了,单个GPU无法承载才去做分开的存储和计算的,减小p的瓶颈就在于设备本身的内存大小
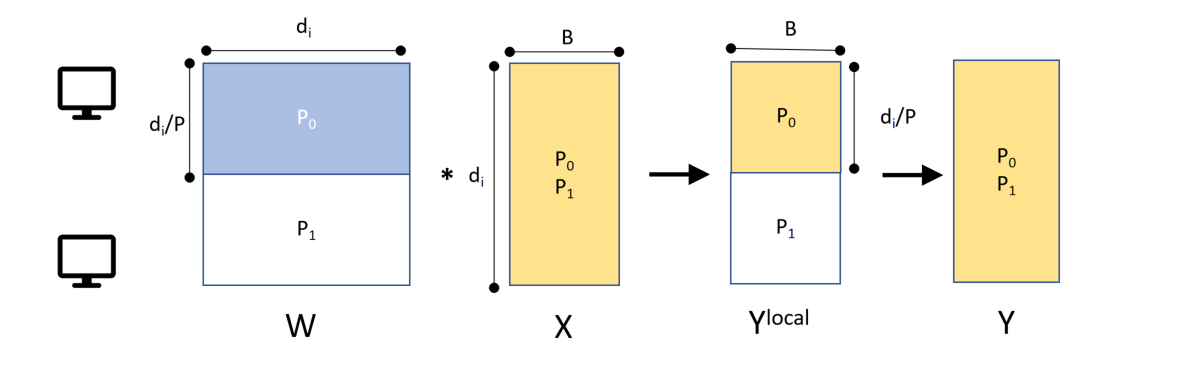
不过还有一个方法,Tensor Parallelism!可以将权重矩阵$W$分给不同的机器,对$x$去计算不同的$W_i$,最后再拼接起来,这样并没有违反矩阵计算的规律,汇总的算法倒是可以借鉴上面的Ring AllReduce
Tensor Parallelism的通信代价比较高
比较实际的架构为单服务器内部GPU的带宽比较高,使用Tensor并行;而服务器之间的带宽比较低,使用Pipeline
 Ring AllReduce的缺点主要是轮数太多,如果每轮的数据量不多的话其实没什么优势,而且其实在Python的浮点数计算中其实加法是不能结合律的,不同的顺序会有不同的结果,会造成细微的差别!但是这并不影响Ring AllReduce是一个非常好的分布式MR架构
Ring AllReduce的缺点主要是轮数太多,如果每轮的数据量不多的话其实没什么优势,而且其实在Python的浮点数计算中其实加法是不能结合律的,不同的顺序会有不同的结果,会造成细微的差别!但是这并不影响Ring AllReduce是一个非常好的分布式MR架构